트리
- 한 노드가 여러 노드를 가르킬 수 있음
- 비 선형적 자료구조
- 그래프
- 데이터 구조의 계층적인 표현
- root는 단 한개만 존재
- 부모 자식 관계 존재
- 트리 안에 트리가 있는 sub tree 구조




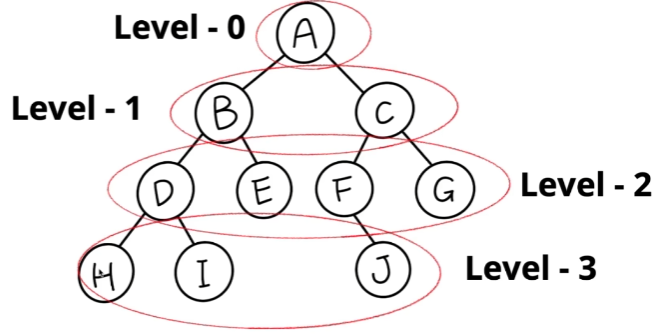

트리
- 이진 트리
- AVL 트리, 레드-블랙 트리
- B-트리, B+트리
- 세그먼트 트리
- 트라이
이진 트리
- 각 노드가 최대 2개의 자식 노드를 가지는 트리
정 이진 트리 (full binary tree)
- 모든 노드가 2개의 자식을 가지거나 자식이 없을 때

포화 이진 트리 (Perfect Binary tree)
- 모든 노드가 2개의 자식을 가지고 leaf 노드가 같은 레벨일때
- 높이가 h인 포화 이진 트리에서 노드 개수는 2^h -1 (root때문에 1개 빼줌)
- Leaf 노드 개수는 2^h

완전 이진 트리
- 마지막 레벨을 제외하고 모든 노드가 채워져야 함
- 노드는 왼쪽에서 오른쪽으로 채워짐
이진트리는 일차원 배열로 표현이 가능하다.


이진 트리의 응용
- 힙
- 이진 탐색 트리
- B-tree
- AVL tree
이진 트리의 기본 연산
- 트리에 데이터 삽입하기
- 데이터 삭제 하기
- 데이터 검색하기
- 트리 탐색 하기
트리 순회
- 트리 구조에서 각 노드를 한 번 씩 방문하는 과정
- 전위 탐색
- 중위 탐색
- 후위 탐색
전위탐색
- 루트 노드 방문
- 왼쪽 서브 트리를 전위 탐색
- 오른쪽 서브 트리를 전위 탐색
중위탐색
- 왼쪽 서브트리 중위탐색
- 루트 노드 방문
- 오른쪽 서브트리 중위탐색
후위탐색
- 왼쪽 서브트리를 후위탐색
- 오른쪽 서브트리를 후위탐색
- 루트 노드 방문
노드를 방문하는 순서 차이가 중요함

이진 탐색 트리 BST
이진트리
- 노드의 왼쪽 서브 트리에는 루트 노드보다 작은 값들만
- 노드의 오른쪽 서브 트리에는 루트 노드보다 큰 값들만
- 서브 트리는 다시 이진 탐색 트리
- 중복된 값은 없다.

최소값은 트리의 맨 왼쪽 값, 오른쪽 값은 최대 값이 된다.


이진 탐색트리의 삽입
- 중복 데이터는 삽입 X
- 추가된 노드는 트리의 leaf에 삽입
이진 트리의 삭제
1. 삭제할 데이터가 leaf 면 그냥 삭제
2. 한 개의 자식 노드를 가질 경우 그냥 삭제 후 올림
3. 두 개의 자식 노드를 가질 경우
- 왼쪽 서브 트리의 최댓값과 교체
- 오른쪽 서브 트리의 최솟값과 교체
'자료구조&알고리즘' 카테고리의 다른 글
| 그래프(Graph) 자료구조 (0) | 2022.04.08 |
|---|---|
| 힙 Heap 자료구조 (0) | 2022.04.08 |
| 탐색과 정렬 알고리즘 (이진 탐색, 버블 정렬, 삽입 정렬, 합병 정렬, 퀵 정렬) (0) | 2022.04.08 |
| HASH와 HASH Collision 그리고 Chaining (해시 자료구조) (0) | 2022.04.07 |
| 스택과 큐에 대하여 (0) | 2022.04.07 |