해시의 예시
회원정보
사진 : 홍길동의 사진
이름 :홍길동
나이 :20
전화번호 : 01012345678
이렇게 12칸의 서랍중 홍길동의 회원정보가 담긴 곳을 항상 매번 찾으면 힘드니까
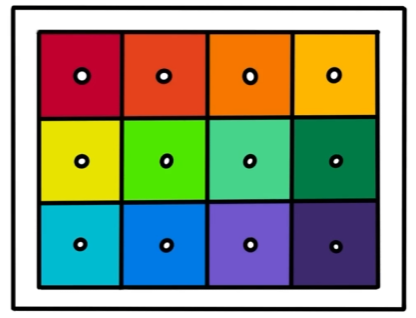
홍길동의 사진 -> 고유의 회원정보 찾아주는 함수 -> 항상 일정한 12가지 색 중 하나로 반환
따라서
KEY : 홍길동의 사진
VALUE: 홍길동의 회원정보가 들어있는 서랍
해시 테이블
- Key, Value로 값을 저장
- 데이터간 순서 존재 X
Hashing - Key
- 키를 기준으로 값을 매핑
- 고유한 값 (중복 X)
Hashing Function -> 임의의 데이터를 특정 값으로 매핑시키는 함수
좋은 해시 함수?
- 키 값을 고르게 분포 시킨다
- 빠른 계산
- 충돌을 최소화
해시 충돌?
- 키 값이 다른데 해시 함수의 결과 값이 동일한 경우

- 충돌이 발생하면 chaining이라는 방식으로 해결
Hash Function 구현

해시 function을 잘 만드려면, 어떤값이 들어왔을때 해쉬 함수가 리턴하는 값이 최대한 충돌하지 않도록 만드는게 중요하다. 여기선 일단 modulo 함수를 통해서 구현하였다.
만약 key가 "abc" 라는 문자열이 들어온다면 아스키코드 값인 97, 98, 99 의 값을 모두 더한뒤 bucketSize로 나눈 나머지를 return 하게 된다. 여기서 bucketSize는 해쉬 table의 size이다.
만약 bucketSize가 1024라고 가정하면 어떤 문자열이 들어오면 그 문자열의 단어 하나하나를 모두 다 더하고, 그 값을 1024로 나눈 나머지의 값을 리턴하게 되는 것이다. 이러면 리턴 값은 0~1023의 값만 가지게 될 것이다.
해시 충돌 Hash Collision

- 해시 충돌은 필연적으로 나타남
- 따라서 최소화 하는 것을 목표로 해야함
비둘기 집 원리
- N+1 개의 물건을 N개의 상자에 넣을 때 적어도 한 상자에는 두 개 이상의 물건이 들어있다.
HashTable size보다 많은 key-value데이터라면, 해시 충돌은 필연적임!
Birthday Problem
-임의의 사람 N명이 모였을 때 그 중에 생일이 같은 두 명이 존재할 확률
- 생일 가짓수 366개 (2/29)
- 실제로는 23명만 나와도 50.7%의 확률로 존재
- 50명은 97%
-> 충돌할 가능성이 충분히 높다 (인덱스가 다 채워지지 않아도)
해시 충돌을 막는 Chaining

- 해시 chaining으로 해시 충돌을 막는다면, 원래 해시의 시간 복잡도인 O (1) 에서 O (n)으로 늘어난다.
- 최근에서는 tree 자료구조를 이용하여 시간을 단축 시켰음
Open Addressing
- 선형 탐색
- 해시 충돌 시 n 칸을 건너뛴 다음 버킷에 저장
- 계산 단순
- 검색 시간이 많이 소요
- 데이터들이 특정 위치에만 밀집
- 데이터 밀집은 성능을 저하시킨다.
제곱탐색
- N^2 칸을 건너뛴 버킷에 데이터를 저장
- 데이터들이 특정 위치에 밀집하는 문제 해결
- 하지만 처음 해시 값이 같다면 여전히 발생
이중해시
- 해시 값에 다른 해시 함수를 한번 더 적용
- hash func 1 : 최초의 해시 값
- hash func 2 : 충돌 발생 시 이동 폭을 구한다.
최초 해시 값이 같더라도 이동 폭이 다르기 떄문에 Clustering 문제 해결 가능 (밀집 문제)
'자료구조&알고리즘' 카테고리의 다른 글
| 트리 자료구조 (이진트리) (0) | 2022.04.08 |
|---|---|
| 탐색과 정렬 알고리즘 (이진 탐색, 버블 정렬, 삽입 정렬, 합병 정렬, 퀵 정렬) (0) | 2022.04.08 |
| 스택과 큐에 대하여 (0) | 2022.04.07 |
| Double Linked List (이중 연결 리스트) (0) | 2022.04.07 |
| 리스트 - LinkedList (0) | 2022.04.07 |